Mudassir Shabbir
Associate Professor, Information Technology University, Theory Group
mudassir.shabbir [AT] itu.edu.pk
Bio
Dr. Mudassir Shabbir is a distinguished figure in the field of machine learning, currently serving as an Associate Professor and Chairperson at the Department of Computer Science at the Information Technology University in Lahore, Pakistan. With a rich academic background, Dr. Shabbir earned his Ph.D. from the Division of Computer Science at Rutgers University, NJ, USA, in 2014. Prior to his current position, Dr. Shabbir held the role of Research Assistant Professor at Vanderbilt University, Nashville, TN. His diverse professional journey includes significant contributions at esteemed institutions such as Lahore University of Management Sciences in Pakistan, Los Alamos National Labs in NM, Bloomberg L.P. in New York, NY, and Rutgers University. Throughout his career, Dr. Shabbir has been recognized for his excellence, being honored as the Rutgers Honors Fellow for the academic year 2011–12. His primary research focus lies in Graph Machine Learning and Robustness in Networks. Driven by a passion for innovation, his work extends to diverse applications, including establishing connections between the physiology and anatomy of the brain network through the analysis of brain fMRI data. Additionally, he has made substantial contributions to the field of social network analysis. Dr. Shabbir's expertise is not limited to theoretical research; he has also delved into the practical realm of Resilient Network Systems. His contributions in this domain involve the application of novel techniques in algorithmic and discrete geometry. Notably, he has developed pioneering methods for the characterization and computation of succinct representations of large datasets, with direct applications in non-parametric statistical analysis. As a thought leader in the machine learning community, Dr. Mudassir Shabbir continues to shape the landscape of the field through his cutting-edge research, fostering innovation, and contributing to the advancement of knowledge in Graph Machine Learning, Robust Networks, and Resilient Network Systems. His multidimensional expertise reflects a commitment to pushing the boundaries of what is possible in the intersection of computer science and machine learning
Recent
- Area Chair #NeurIPS2023
- Area Chair #CVPR2023
- Paper accepted in #NeurIPS2022
- Talk at AI-connect by Motive titled "Mapping Economic Wellbeing"
- Reviewer for ICCV 2023, CVPR 2022, ECCV 2022, CHI 2022
- Malaria detection work accepted at CVPR 2022
- Domain Adaptation work accepted at NeurIPS 2021
- Groogle Reseach Scholar Award 2021
- AI for Earth innovation program by National Geographic & Microsoft 2021, co-PI
- Outstanding Reviewer for CVPR 2021
- Second PhD student clears proposal stage [Dec 2020]
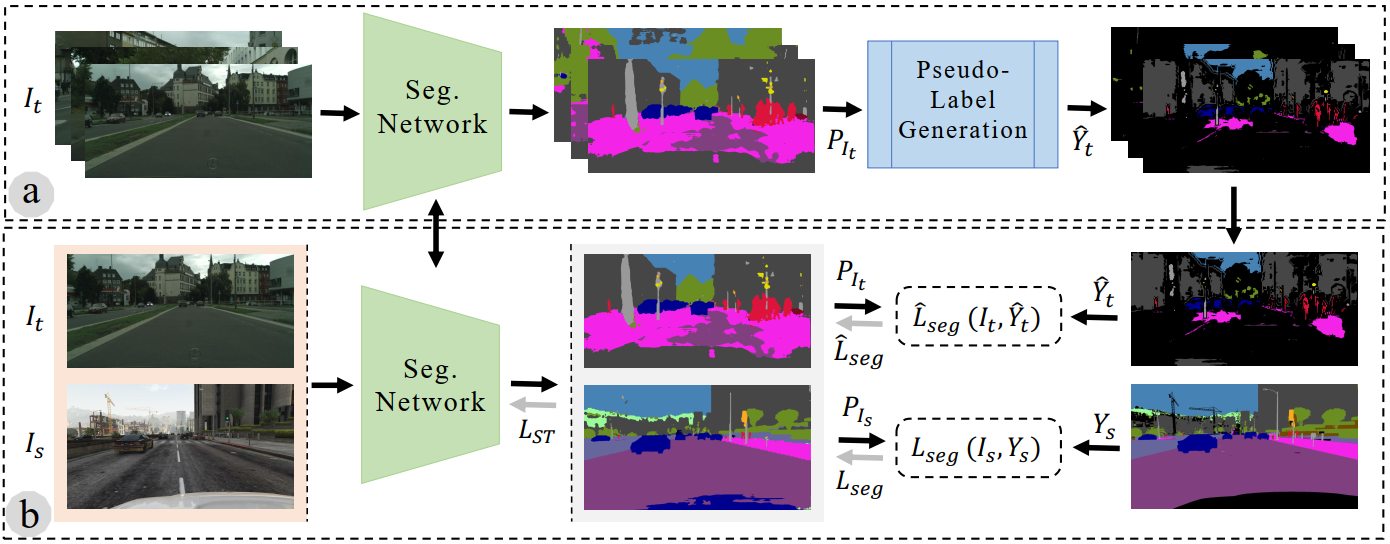
- Work on exploiting scale invariance in the source domain, to regulate adaptation accepted at #ECCV2020.We believe it was 1st time work completely done in Pakistan was accepted in this venue. [2020]
- Presented in Change Seminar, University of Washington [2020]
Publications
Most recent publications on Google Scholar.
‡ indicates equal contribution.
- Sequential Graph Neural Networks for Source Code Vulnerability Identification
ArXiv (2023)
Vulnerability identification constitutes a task of high importance for cyber security. It is quite helpful for locating and fixing vulnerable functions in large applications. However, this task is rather challenging owing to the absence of reliable and adequately managed datasets and learning models. Existing solutions typically rely on human expertise to annotate datasets or specify features, which is prone to error. In addition, the learning models have a high rate of false positives. To bridge this gap, in this paper, we present a properly curated C/C++ source code vulnerability dataset, denoted as CVEFunctionGraphEmbeddings (CVEFGE), to aid in developing models. CVEFGE is automatically crawled from the CVE database, which contains authentic and publicly disclosed source code vulnerabilities. We also propose a learning framework based on graph neural networks, denoted SEquential Graph Neural Network (SEGNN) for learning a large number of code semantic representations. SEGNN consists of a sequential learning module, graph convolution, pooling, and fully connected layers. Our evaluations on two datasets and four baseline methods in a graph classification setting demonstrate state-of-the-art results.
- Learning-Based Heuristic for Combinatorial Optimization of the Minimum Dominating Set Problem using Graph Convolutional Networks
ArXiv (2023)
A dominating set of a graph $\mathcal{G=(V, E)}$ is a subset of vertices $S\subseteq\mathcal{V}$ such that every vertex $v\in \mathcal{V} \setminus S$ outside the dominating set is adjacent to a vertex $u\in S$ within the set. The minimum dominating set problem seeks to find a dominating set of minimum cardinality and is a well-established NP-hard combinatorial optimization problem. We propose a novel learning-based heuristic approach to compute solutions for the minimum dominating set problem using graph convolutional networks. We conduct an extensive experimental evaluation of the proposed method on a combination of randomly generated graphs and real-world graph datasets. Our results indicate that the proposed learning-based approach can outperform a classical greedy approximation algorithm. Furthermore, we demonstrate the generalization capability of the graph convolutional network across datasets and its ability to scale to graphs of higher order than those on which it was trained. Finally, we utilize the proposed learning-based heuristic in an iterative greedy algorithm, achieving state-of-the-art performance in the computation of dominating sets.
- NeuroGraph: Benchmarks for Graph Machine Learning in Brain Connectomics
ArXiv (2023)
Machine learning provides a valuable tool for analyzing high-dimensional functional neuroimaging data, and is proving effective in predicting various neurological conditions, psychiatric disorders, and cognitive patterns. In functional Magnetic Resonance Imaging (MRI) research, interactions between brain regions are commonly modeled using graph-based representations. The potency of graph machine learning methods has been established across myriad domains, marking a transformative step in data interpretation and predictive modeling. Yet, despite their promise, the transposition of these techniques to the neuroimaging domain remains surprisingly under-explored due to the expansive preprocessing pipeline and large parameter search space for graph-based datasets construction. In this paper, we introduce NeuroGraph, a collection of graph-based neuroimaging datasets that span multiple categories of behavioral and cognitive traits. We delve deeply into the dataset generation search space by crafting 35 datasets within both static and dynamic contexts, running in excess of 15 baseline methods for benchmarking. Additionally, we provide generic frameworks for learning on dynamic as well as static graphs. Our extensive experiments lead to several key observations. Notably, using correlation vectors as node features, incorporating larger number of regions of interest, and employing sparser graphs lead to improved performance. To foster further advancements in graph-based data driven Neuroimaging, we offer a comprehensive open source Python package that includes the datasets, baseline implementations, model training, and standard evaluation. The package is publicly accessible at https://anwar-said.github.io/anwarsaid/neurograph.html .
- Resilient Multi-agent Reinforcement Learning Using Medoid and Soft-medoid Based Aggregation
2022 IEEE International Conference on Assured Autonomy (ICAA) (2022)
A network of reinforcement learning (RL) agents that cooperate with each other by sharing information can improve learning performance of control and coordination tasks when compared to non-cooperative agents. However, networked Multi-agent Reinforcement Learning (MARL) is vulnerable to adversarial agents that can compromise some agents and send malicious information to the network. In this paper, we consider the problem of resilient MARL in the presence of adversarial agents that aim to compromise the learning algorithm. First, the paper presents an attack model which aims to degrade the performance of a target agent by modifying the parameters shared by an attacked agent. In order to improve the resilience, the paper presents aggregation methods using medoid and soft-medoid. Our analysis shows that the medoid-based MARL algorithms converge to an optimal solution given standard assumptions, and improve the overall learning performance and robustness. Simulation results show the effectiveness of the aggregation methods compared with average and median-based aggregation.
- What a drag! Streamlining the UAV design process with design grammars and drag surrogates
(2022)
—Unmanned Aerial Vehicles (UAVs) continue to pro- liferate, revolutionizing tasks such as cargo transport, surveil-lance, and search and rescue operations. With the discovery of novel use cases or specialized tasks for aerial vehicles, there is an increased need for improved design space exploration and performance estimation techniques for candidate UAV designs. Typical pipelines for this design process rely on time-consuming human efforts to identify productive design geometries or expensive computational approaches for performance analysis to reconcile aerodynamic, electrical, and physical interactions. In this work-in-progress paper, we propose the use of a design process that uses a design grammar for UAV design generation and a Graph Neural Network (GNN)-based drag surrogate trained on simulation data for accelerated UAV design space exploration. We formulate a UAV design grammar and provide preliminary performance results from the GNN drag surrogate for randomly generated designs. We expect our approach to accelerate the exploration of UAV design geometries using a learned surrogate drag model to circumvent resource-hungry Computer-aided design (CAD) and simulation routines.
- Attack-Resilient Multi-Agent Flocking Control Using Graph Neural Networks
2022 30th Mediterranean Conference on Control and Automation (MED) (2022)
Flocking control of a group of mobile agents has been recently investigated using Graph Convolution Networks (GCNs). The design relies on training using a centralized controller but the resulting GCN controller is based on communication between the agents. The agents receive sensor measurements which are incorporated into the states and shared between the neighbors. However, the paradigm is prone to adversarial attacks. In this paper, we consider the problem of designing GCN-based distributed flocking control that is resilient to attacks on the communicated information. We consider an attack model that is used to compromise the inter-agent communication and may inject arbitrary signals. Our control design uses a coordinate-wise median-based aggregation function. It is shown that the GCN-based controller using the proposed aggregation method is resilient against attacks on the communication between the agents, whereas the typical average-based aggregation fails to maintain the flock structure. Robustness analysis is performed to show that the proposed method is resilient whenever a majority of the agents in the neighborhood can be trusted. Simulation results and analysis are presented that validate the merits of the proposed approach.
- Leader Selection for Strong Structural Controllability in Networks using Zero Forcing Sets
2022 American Control Conference (ACC) (2022)
This paper studies the problem of computing a minimum zero forcing set (ZFS) in graphs. The problem is important because it is directly related to the leader selection problem for the strong structural controllability of networks defined over graphs. Computing a ZFS of minimum size is a well-known NP-hard problem in general. We show that previously known greedy heuristic could give arbitrarily bad solutions for some graphs. We study the problem on trees and present an optimal algorithm to compute a minimum ZFS in linear time in trees. For general graphs, we present a game-theoretic solution by formalizing the minimum ZFS problem as a potential game. Finally, we numerically evaluate our results on random graphs.
- Byzantine Resilient Distributed Learning in Multirobot Systems
IEEE Transactions on Robotics (2022)
Distributed machine learning algorithms are increasingly used in multirobot systems and are prone to Byzantine attacks. In this article, we consider a distributed implementation of the stochastic gradient descent (SGD) algorithm in a cooperative network, where networked agents optimize a global loss function using SGD on the local data and aggregation of the estimates of immediate neighbors. Byzantine agents can send arbitrary estimates to their neighbors, which may disrupt the convergence of normal agents to the optimum state. We show that if every normal agent combines its neighbors’ estimates (states) such that the aggregated state is in the convex hull of its normal neighbors’ states, then the resilient convergence is guaranteed. To assure this sufficient condition, we propose a resilient aggregation rule based on the notion of centerpoint, which is a generalization of the median in the higher-dimensional Euclidean space. We evaluate our results using examples of target pursuit and pattern recognition in multirobot systems. The evaluation results demonstrate that distributed learning with average, coordinate-wise median, and geometric median-based aggregation rules fail to converge to the optimum state, whereas the centerpoint-based aggregation rule is resilient in the same scenario.
- Edge Augmentation With Controllability Constraints in Directed Laplacian Networks
IEEE Control Systems Letters (2021)
In this letter, we study the maximum edge augmentation problem in directed Laplacian networks to improve their robustness while preserving lower bounds on their strong structural controllability (SSC). Since adding edges could adversely impact network controllability, the main objective is to maximally densify a given network by selectively adding missing edges while ensuring that SSC of the network does not deteriorate beyond certain levels specified by the SSC bounds. We consider two widely used bounds: first is based on the notion of zero forcing (ZF), and the second relies on the distances between nodes in a graph. We provide an edge augmentation algorithm that adds the maximum number of edges in a graph while preserving the ZF-based bound, and also derive a closed-form expression for the exact number of edges added to the graph. Then, we examine the edge augmentation while preserving the distance-based bound and present a randomized algorithm that guarantees an $\alpha $ –approximate solution with high probability. Finally, we numerically evaluate and compare these edge augmentation solutions.
- Resilient Distributed Vector Consensus Using Centerpoint (cid:63)
(2021)
In this paper, we study the resilient vector consensus problem in networks with adversarial agents and improve resilience guarantees of existing algorithms. A common approach to achieving resilient vector consensus is that every non-adversarial (or normal) agent in the network updates its state by moving towards a point in the convex hull of its normal neighbors’ states. Since an agent cannot distinguish between its normal and adversarial neighbors, computing such a point, often called as safe point , is a challenging task. To compute a safe point, we propose to use the notion of centerpoint , which is an extension of the median in higher dimensions, instead of Tverberg partition of points, which is often used for this purpose. We discuss that the notion of centerpoint provides a complete characterization of safe points in R d . In particular, we show that a safe point is essentially an interior centerpoint if the number of adversaries in the neighborhood of a normal agent i is less than N i d +1 , where d is the dimension of the state vector and N i is the total number of agents in the neighborhood of i . Consequently, we obtain necessary and sufficient conditions on the number of adversarial agents to guarantee resilient vector consensus. Further, by considering the complexity of computing centerpoints, we discuss improvements in the resilience guarantees of vector consensus algorithms and compare with the other existing approaches. Finally, we numerically evaluate the performance of our approach through experiments.
- Computing Graph Descriptors on Edge Streams
ACM Transactions on Knowledge Discovery from Data (2021)
Feature extraction is an essential task in graph analytics. These feature vectors, called graph descriptors, are used in downstream vector-space-based graph analysis models. This idea has proved fruitful in the past, with spectral-based graph descriptors providing state-of-the-art classification accuracy. However, known algorithms to compute meaningful descriptors do not scale to large graphs since: (1) they require storing the entire graph in memory, and (2) the end-user has no control over the algorithm’s runtime. In this article, we present streaming algorithms to approximately compute three different graph descriptors capturing the essential structure of graphs. Operating on edge streams allows us to avoid storing the entire graph in memory, and controlling the sample size enables us to keep the runtime of our algorithms within desired bounds. We demonstrate the efficacy of the proposed descriptors by analyzing the approximation error and classification accuracy. Our scalable algorithms compute descriptors of graphs with millions of edges within minutes. Moreover, these descriptors yield predictive accuracy comparable to the state-of-the-art methods but can be computed using only 25% as much memory.
- SEMOUR: A Scripted Emotional Speech Repository for Urdu
Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems (2021)
Designing reliable Speech Emotion Recognition systems is a complex task that inevitably requires sufficient data for training purposes. Such extensive datasets are currently available in only a few languages, including English, German, and Italian. In this paper, we present SEMOUR, the first scripted database of emotion-tagged speech in the Urdu language, to design an Urdu Speech Recognition System. Our gender-balanced dataset contains 15,040 unique instances recorded by eight professional actors eliciting a syntactically complex script. The dataset is phonetically balanced, and reliably exhibits a varied set of emotions as marked by the high agreement scores among human raters in experiments. We also provide various baseline speech emotion prediction scores on the database, which could be used for various applications like personalized robot assistants, diagnosis of psychological disorders, and getting feedback from a low-tech-enabled population, etc. On a random test sample, our model correctly predicts an emotion with a state-of-the-art 92% accuracy.
- Resilient Distributed Diffusion for Multi-Robot Systems Using Centerpoint
Robotics: Science and Systems XVI (2020)
—In this paper, we study the resilient diffusion prob- lem in a network of robots aiming to perform a task by optimizing a global cost function in a cooperative manner. In distributed diffusion, robots combine the information collected from their local neighbors and incorporate this aggregated information to update their states. If some robots are adversarial, this cooperation can disrupt the convergence of robots to the desired state. We propose a resilient aggregation rule based on the notion of centerpoint , which is a generalization of the median in the higher dimensional Euclidean space. Robots exchange their d dimensional state vectors with neighbors. We show that if a normal robot implements the centerpoint-based aggregation rule and has n neighbors, of which at most (cid:100) nd +1 (cid:101)− 1 are adversarial, then the aggregated state always lies in the convex hull of the states of the normal neighbors of the robot. Consequently, all normal robots implementing the distributed diffusion algorithm converge resiliently to the true target state. We also show that commonly used aggregation rules based on the coordinate-wise median and geometric median are, in fact, not resilient to certain attacks. We also numerically evaluate our results on mobile multirobot networks and demonstrate the cases where diffusion with the weighted average, coordinate-wise median, and geometric median-based aggregation rules fail to converge to the true target state, whereas diffusion with the centerpoint-based rule is resilient in the same scenario.
- Graph-Theoretic Approach for Increasing Participation in Networks With Assorted Resources
IEEE Transactions on Network Science and Engineering (2020)
In many cooperative networks, individuals participate actively as long as they recognize a sufficient value in participation, which depends not only on the number, but also on the attributes of other participating members. In this paper, we present a generalized model of individuals’ participation in such networks, and a strategy to maximize the number of participating individuals. Unlike most of the existing literature, our model incorporates both the network structure and the heterogeneity of individuals in terms of their attributes and resources. We consider that each individual possesses a subset of available resources (attributes), which it shares with neighbors as long as neighbors reciprocate and provide the missing resources to the individual. However, individual leaves the network if it cannot find all the resources in its neighborhood. To model this phenomenon, we introduce a graph-theoretic notion of the $(r,s)$-core, which is the sub-network consisting of only those individuals who can access all the resources by collaborating with their neighbors. Since disengagement of an individual could initiate a cascading withdrawal of more individuals from the network, one of our main goals is to prevent this unraveling and maximize the number of participating individuals. For this purpose, we utilize the notion of anchors—individuals that continue to participate (due to incentives) even if they cannot find all of the resources in their neighborhood. By introducing only a few anchors, we can significantly increase the number of participating individuals, which in our model corresponds to increasing the size of the $(r,s)$-core. We formulate and thoroughly analyze the anchors’ selection problem by classifying the cases in which the problem is polynomial-time solvable, NP-complete, and inapproximable. Further, we provide greedy and metaheuristic search algorithms to compute a set of anchors and evaluate our results on various networks. Our results are applicable to a large number of cooperative networking applications, including participatory sensing in which users develop an elaborate knowledge of their environment through sharing measurements.
- Improving Network Robustness through Edge Augmentation While Preserving Strong Structural Controllability
2020 American Control Conference (ACC) (2020)
In this paper, we consider a network of agents with Laplacian dynamics, and study the problem of improving network robustness by adding maximum number of edges within the network while preserving a lower bound on its strong structural controllability (SSC). Edge augmentation increases network’s robustness to noise and structural changes, however, it could also deteriorate network controllability. By exploiting relationship between network controllability and distances between nodes in graphs, we formulate an edge augmentation problem with a constraint to preserve distances between certain node pairs, which in turn guarantees that a lower bound on SSC is maintained even after adding edges. In this direction, first we choose a node pair and maximally add edges while maintaining the distance between selected nodes. We show that an optimal solution belongs to a certain class of graphs called clique chains. Then, we present and analyze two algorithms to add edges while preserving distances between a certain collection of nodes. Finally, we evaluate our results on various networks.
- A Simpler NP-Hardness Proof for Familial Graph Compression
ArXiv (2020)
This document presents a simpler proof showcasing the NP-hardness of Familial Graph Compression.
- Resilient Vector Consensus in Multi-Agent Networks Using Centerpoints
2020 American Control Conference (ACC) (2020)
In this paper, we study the resilient vector consensus problem in multi-agent networks and improve resilience guarantees of existing algorithms. In resilient vector consensus, agents update their states, which are vectors in ℝd, by locally interacting with other agents some of which might be adversarial. The main objective is to ensure that normal (non-adversarial) agents converge at a common state that lies in the convex hull of their initial states. Currently, resilient vector consensus algorithms, such as approximate distributed robust convergence (ADRC) are based on the idea that to update states in each time step, every normal node needs to compute a point that lies in the convex hull of its normal neighbors’ states. To compute such a point, the idea of Tverberg partition is typically used, which is computationally hard. Approximation algorithms for Tverberg partition negatively impact the resilience guarantees of consensus algorithm. To deal with this issue, we propose to use the idea of centerpoint, which is an extension of median in higher dimensions, instead of Tverberg partition. We show that the resilience of such algorithms to adversarial nodes is improved if we use the notion of centerpoint. Furthermore, using centerpoint provides a better characterization of the necessary and sufficient conditions guaranteeing resilient vector consensus. We analyze these conditions in two, three, and higher dimensions separately. We also numerically evaluate the performance of our approach.
- Interplay Between Resilience and Accuracy in Resilient Vector Consensus in Multi-Agent Networks
2020 59th IEEE Conference on Decision and Control (CDC) (2020)
In this paper, we study the relationship between resilience and accuracy in the resilient distributed multidimensional consensus problem. We consider a network of agents, each of which has a state in Rd. Some agents in the network are adversarial and can change their states arbitrarily. The normal (non-adversarial) agents interact locally and update their states to achieve consensus at some point in the convex hull $\mathcal{C}$ of their initial states. This objective is achievable if the number of adversaries in the neighborhood of normal agents is less than a specific value, which is a function of the local connectivity and the state dimension d. However, to be resilient against adversaries, especially in the case of large d, the desired local connectivity is large. We discuss that resilience against adversarial agents can be improved if normal agents are allowed to converge in a bounded region $\mathcal{B} \supseteq \mathcal{C}$, which means normal agents converge at some point close to but not necessarily inside $\mathcal{C}$ in the worst case. The accuracy of resilient consensus can be measured by the Hausdorff distance between $\mathcal{B}$ and $\mathcal{C}$. As a result, resilience can be improved at the cost of accuracy. We propose a resilient bounded consensus algorithm that exploits the trade-off between resilience and accuracy by projecting d-dimensional states into lower dimensions and then solving instances of resilient consensus in lower dimensions. We analyze the algorithm, present various resilience and accuracy bounds, and also numerically evaluate our results.
- Resilient multi-robot target pursuit
Proceedings of the 7th Symposium on Hot Topics in the Science of Security (2020)
We consider the problem of networked agents cooperating together to perform a task of optimizing the parameters of a global cost function. Agents receive linearly correlated noisy streaming data that can be used to learn the target parameters via Least-Mean-Squares (LMS) approaches. Diffusion scheme is incorporated such that at each step after agents adapt the parameters by the current received data, a combination step is included for agents to aggregate the information coming from its one-hop neighbors. It has been demonstrated that by introducing the aggregation step, diffusion algorithms greatly improve the learning accuracy of the parameters measured by the network Mean-Square-Deviation (MSD) [1]. However, the aggregation step is susceptible to attacks. In the presence of Byzantine agents, the aggregation of Byzantine information can easily disrupt the convergence of normal robots and even one Byzantine agent can drive its normal neighbors to converge to some point desired by the attacker [2]. To address this, we propose a resilient aggregation rule based on the notion of centerpoint [3], which is a generalization of median in the higher dimensional Euclidean space. We show that if a normal robot implements the centerpoint based aggregation rule for distributed diffusion, then it can guarantee the aggregated result to lie inside the convex hull of its normal neighbors, given at most [EQUATION] neighbors are Byzantine with n total negihbors and d-dimensional state vectors exchanged among agents. Further, we demonstrate all normal robots implementing centerpoint based distributed diffusion converge resiliently to the true target state. In addition, we demonstrate that widely adopted aggregation rules such as coordinate-wise median [4] and geometric median [5] based are not resilient under certain conditions. The main reason is that unlike centerpoint based aggregation, these rules do not guarantee the aggregation result to be inside the convex hull of the states of normal agents. We carried out experiments on Robotarium, a multirobot testbed developed at the Georgia Institute of Technology to demonstrate the cases where diffusion with coordinate-wise median and geometric median based aggregation rules fail to converge to the true target state, whereas diffusion with centerpoint based rule resiliently converge to the true target state in the same scenario.
- Strong Structural Controllability of Diffusively Coupled Networks: Comparison of Bounds Based on Distances and Zero Forcing
2020 59th IEEE Conference on Decision and Control (CDC) (2020)
We study the strong structural controllability (SSC) of diffusively coupled networks, where the external control inputs are injected to only some nodes, namely the leaders. For such systems, one measure of controllability is the dimension of strong structurally controllable subspace, which is equal to the smallest possible rank of controllability matrix under admissible (positive) coupling weights. In this paper, we compare two tight lower bounds on the dimension of strong structurally controllable subspace: one based on the distances of followers to leaders, and the other based on the graph coloring process known as zero forcing. We show that the distance-based lower bound is usually better than the zero-forcing-based bound when the leaders do not constitute a zero-forcing set. On the other hand, we also show that any set of leaders that can be shown to achieve complete SSC via the distance-based bound is necessarily a zero-forcing set. Furthermore, we present a novel bound based on the combination of these two approaches, which is always at least as good as, and in some cases strictly greater than, the maximum of the two bounds. Finally, we present some numerical results to compare the bounds on various graphs.
- Resilient Distributed Vector Consensus Using Centerpoints
(2020)
In this paper, we study the resilient vector consensus problem in networks with adversarial agents and improve resilience guarantees of existing algorithms. A common approach to achieving resilient vector consensus is that every non-adversarial (or normal) agent in the network updates its state by moving towards a point in the convex hull of its normal neighbors’ states. Since an agent cannot distinguish between its normal and adversarial neighbors, computing such a point, often called as safe point, is a challenging task. To compute a safe point, we propose to use the notion of centerpoint, which is an extension of the median in higher dimensions, instead of Tverberg partition of points, which is often used for this purpose. We discuss that the notion of centerpoint provides a complete characterization of safe points in R. In particular, we show that a safe point is essentially an interior centerpoint if the number of adversaries in the neighborhood of a normal agent i is less than Ni d+1 , where d is the dimension of the state vector and Ni is the total number of agents in the neighborhood of i. Consequently, we obtain necessary and sufficient conditions on the number of adversarial agents to guarantee resilient vector consensus. Further, by considering the complexity of computing centerpoints, we discuss improvements in the resilience guarantees of vector consensus algorithms and compare with the other existing approaches. Finally, we numerically evaluate the performance of our approach through experiments.
- Tradeoff Between Controllability and Robustness in Diffusively Coupled Networks
IEEE Transactions on Control of Network Systems (2020)
In this article, we demonstrate a conflicting relationship between two crucial properties—
controllability androbustness —in linear dynamical networks of diffusively coupled agents. In particular, for any given number of nodes$N$ $D$ $N$ $D$ $N$ $D$ $N$ $D$ $N$ $D$ - Computation of the Distance-Based Bound on Strong Structural Controllability in Networks
IEEE Transactions on Automatic Control (2019)
In this article, we study the problem of computing a tight lower bound on the dimension of the strong structurally controllable subspace (SSCS) in networks with Laplacian dynamics. The bound is based on a sequence of vectors containing the distances between leaders (nodes with external inputs) and followers (remaining nodes) in the underlying network graph. Such vectors are referred to as the distance-to-leaders vectors. We give exact and approximate algorithms to compute the longest sequences of distance-to-leaders vectors, which directly provide distance-based bounds on the dimension of SSCS. The distance-based bound is known to outperform the other known bounds (for instance, based on zero-forcing sets), especially when the network is partially strong structurally controllable. Using these results, we discuss an application of the distance-based bound in solving the leader selection problem for strong structural controllability. Further, we characterize strong structural controllability in path and cycle graphs with a given set of leader nodes using sequences of distance-to-leaders vectors. Finally, we numerically evaluate our results on various graphs.
- Structural Robustness to Noise in Consensus Networks: Impact of Average Degrees and Average Distances
2019 IEEE 58th Conference on Decision and Control (CDC) (2019)
We investigate how the graph topology influences the robustness to noise in undirected linear consensus networks. We consider the expected steady state population variance of states as the measure of vulnerability to noise. We quantify the structural robustness of a network by using the smallest value this measure can attain under edge weights from the unit interval. Our main result shows that the average distance between nodes and the average node degree define tight upper and lower bounds on the structural robustness. Using these bounds, we characterize the networks with different types of robustness scaling. We also present a fundamental trade-off between the structural robustness and the sparsity of networks. We then show that random regular graphs typically have near-optimal structural robustness among the graphs with same size and average degree. Some simulation results are also provided.
- On the Trade-off Between Controllability and Robustness in Networks of Diffusively Coupled Agents
2019 American Control Conference (ACC) (2019)
In this paper, we study the relationship between two crucial properties in linear dynamical networks of diffusively coupled agents, that is controllability and robustness to noise and structural changes in the network. In particular, for any given network size and diameter, we identify networks that are maximally robust and then analyze their strong structural controllability. We do so by determining the minimum number of leaders to make such networks completely controllable with arbitrary coupling weights between agents. Similarly, we design networks with the same given parameters that are completely controllable independent of coupling weights through a minimum number of leaders, and then also analyze their robustness. We utilize the notion of Kirchhoff index to measure network robustness to noise and structural changes. Our controllability analysis is based on novel graph-theoretic methods that offer insights on the important connection between network robustness and strong structural controllability in such networks.
- On the Computation of the Distance-based Lower Bound on Strong Structural Controllability in Networks
2019 IEEE 58th Conference on Decision and Control (CDC) (2019)
A network of agents with linear dynamics is strong structurally controllable if agents can be maneuvered from any initial state to any final state independently of the coupling strengths between agents. If a network is not strong structurally controllable with given input nodes (leaders), then the dimension of strong structurally controllable subspace quantifies the extent to which a network can be controlled by the same inputs. Computing this dimension exactly is computationally challenging. In this paper, we study the problem of computing a sharp lower bound on the dimension of strong structurally controllable subspace in networks with Laplacian dynamics. The bound is based on a sequence of vectors containing distances between leaders and the remaining nodes in the underlying network graph. Such vectors are referred to as the distance-to-leader vectors. We provide a polynomial time algorithm to compute a desired sequence of distance-to-leader vectors with a fixed set of leaders, which directly provides a lower bound on the dimension of strong structurally controllable subspace. We also present a linearithmic approximation algorithm to compute such a sequence, which provides near optimal solutions in practice. Finally, we numerically evaluate and compare our bound with other bounds in the literature on various networks.
- Structural Robustness to Noise in Consensus Networks: Impact of Degrees and Distances, Fundamental Limits, and Extremal Graphs
IEEE Transactions on Automatic Control (2019)
We investigate how the graph topology influences the robustness to noise in undirected linear consensus networks. We measure the structural robustness by using the smallest possible value of steady-state population variance of states under the noisy consensus dynamics with edge weights from the unit interval. We derive tight upper and lower bounds on the structural robustness of networks based on the average distance between nodes and the average node degree. Using the proposed bounds, we characterize the networks with different types of robustness scaling under increasing size. Furthermore, we present a fundamental tradeoff between the structural robustness and the average degree of networks. While this tradeoff implies that a desired level of structural robustness can only be achieved by graphs with a sufficiently large average degree, we also show that there exist dense graphs with poor structural robustness. We then show that random
$k$ $k$ $n$ $n$ $k$ $n$ $k$ $k$ $n$ $k$ - Affine-Invariant Outlier Detection and Data Visualization
None (2017)
A wealth of data is generated daily by social media websites that is an essential component of the Big Data Revolution . In many cases, the data is anonymized before being disseminated for research and analysis. This anonymization process distorts the data so that some essential characteristics are lost which may not be captured by methods that are not robust against such transformations. In this paper we propose novel algorithms, for two-dimensional data, for a recently discovered statistical data analysis measure, the Ray Shooting Depth (RSD) that provides an affine-invariant ranking of data points. In addition, we prove some complexity results and illustrate some of the desirable properties of RSD via comparisons with other similar notions. We develop an open-source data visualization tool based on RSD, and show its applications in distribution estimation, outlier detection, and D tolerance-region construction.
- Scalable Approximation Algorithm for Network Immunization
None (2017)
The problem of identifying important players in a given network is of pivotal importance for viral marketing, public health management, network security and various other fields of social network analysis. In this work we find the most important vertices in a graph G = (V,E) to immunize so as the chances of an epidemic outbreak is minimized. This problem is directly relevant to minimizing the impact of a contagion spread (e.g. flu virus, computer virus and rumor) in a graph (e.g. social network, computer network) with a limited budget (e.g. the number of available vaccines, antivirus software, filters). It is well known that this problem is computationally intractable (it is NP-hard). In this work we reformulate the problem as a budgeted combinational optimization problem and use techniques from spectral graph theory to design an efficient greedy algorithm to find a subset of vertices to be immunized. We show that our algorithm takes less time compared to the state of the art algorithm. Thus our algorithm is scalable to networks of much larger sizes than best known solutions proposed earlier. We also give analytical bounds on the quality of our algorithm. Furthermore, we evaluate the efficacy of our algorithm on a number of real world networks and demonstrate that the empirical performance of algorithm supplements the theoretical bounds we present, both in terms of approximation guarantees and computational efficiency.
- Spectral Methods for Immunization of Large Networks
ArXiv (2017)
Given a network of nodes, minimizing the spread of a contagion using a limited budget is a well-studied problem with applications in network security, viral marketing, social networks, and public health. In real graphs, virus may infect a node which in turn infects its neighbor nodes and this may trigger an epidemic in the whole graph. The goal thus is to select the best k nodes (budget constraint) that are immunized (vaccinated, screened, filtered) so as the remaining graph is less prone to the epidemic. It is known that the problem is, in all practical models, computationally intractable even for moderate sized graphs. In this paper we employ ideas from spectral graph theory to define relevance and importance of nodes. Using novel graph theoretic techniques, we then design an efficient approximation algorithm to immunize the graph. Theoretical guarantees on the running time of our algorithm show that it is more efficient than any other known solution in the literature. We test the performance of our algorithm on several real world graphs. Experiments show that our algorithm scales well for large graphs and outperforms state of the art algorithms both in quality (containment of epidemic) and efficiency (runtime and space complexity).
- k-Centerpoints Conjectures for Pointsets in ℝd
Int. J. Comput. Geom. Appl. (2015)
In this paper, we introduce the notion of k-centerpoints for any set P of n points in ℝd. These unify and generalize previous results such as the classical centerpoint theorem,1 and the recently-proven ray-shooting theorem.2 We define two variants: affine k-centerpoints, and topological k-centerpoints. We prove their equivalence in ℝ2, and conjecture that these are in fact equivalent in any dimension. We present the first non-trivial bounds for these problems in ℝd, as well as present several conjectures related to them.
- SOME RESULTS IN COMPUTATIONAL AND COMBINATORIAL GEOMETRY
(2014)
OF THE DISSERTATION Some Results in Computational and Combinatorial Geometry by Mudassir Shabbir Dissertation Director: William Steiger In this thesis we present some new results in the field of discrete and computational geometry. The techniques and tools developed to achieve these results add to our understanding of important geometric objects like line arrangements, and geometric measures of depth. Small Hitting Sets Given a set S of n points, a weak -net X is a set of points (not necessarily in S) such that any convex set, called a range, that contains more than an fraction of S must meet X for a fixed > 0 [30]. Aronov et al. gave the first bounds on when the cardinality of X is a fixed small number in the plane. Later Mustafa and Ray proved that |X| = 2 can be chosen so that we hit all convex ranges that contain 4n/7 points of S [46]. We describe an O(n log n) time algorithm to find points z1 6= z2, at least one of which must meet any convex set of “size” greater than 4n/7; z1 and z2 comprise a hitting set of size two for such convex ranges. This is the first algorithm for computing the hitting sets of fixed size.
- Ray-Shooting Depth in R 2 - Algorithms and Applications
(2011)
The notion of Ray Shooting Depth was introduced in recent papers of Gromov, and of Fox, Gromov, Laorgue, Naor, and Pach. It played a key role in their results. It also represents a new concept for data depth in R d and oers interesting possibilities for applications. Here, we study some computational aspects of ray-shooting depth in dimension two via algorithms and some complexity results. In addition we advocate the use of ray-shooting depth in statistical data analysis and in other applications. We illustrate some of the desireable properties via comparisons with other notions of depth.
- Acceleration of Smith-Waterman using Recursive Variable Expansion
2008 11th EUROMICRO Conference on Digital System Design Architectures, Methods and Tools (2008)
The Smith-Waterman (SW) algorithm is a local sequence alignment algorithm that attempts to align two biological sequences of varying length such that the alignment score is maximum. In this paper, we propose a new approach to reduce the time needed to perform the SW algorithm. This is done by applying the concept of recursive variable expansion, which exposes more parallelism in the algorithm than any other published method. The paper estimates the speed and hardware overhead for the newly proposed approach relative to other known acceleration methods. Using the new approach, it is possible to achieve a minimum speedup of 400 times better than the serial case for a typical sequence length of 500, which is 1.6 times higher than any other published method. The paper also shows that further speedup can be achieved using extra hardware to expose even more parallelism in the algorithm.
- Acceleration of Biological Sequence Alignment using Recursive Variable Expansion
(2007)
Biological sequence alignment is one of the most important problems in computational biology. Given two sequences of varying length are aligned such that the alignment score i s maximum. The alignment score is calculated based on the number of matches, mismatches and gaps in the alignment suggest d. The basic sequence alignment algorithms are Needleman-Wun sch (NW) algorithm and Smith-Waterman (SW) algorithm, which find the optimal global and local alignment, respectively. I n this paper, we have accelerated the Needleman-Wunsch by applyin g the Recursive Variable Expansion partially, which can be ea sily implemented on FPGA. This method extract more parallelism than other prevalent parallel implementations and we are able to achieve a speed up of 1.55 times.
- Efficient Approximation Algorithms for String Kernel Based Sequence Classification
(2017)
Sequence classification algorithms, such as SVM, require a definition of distance (similarity) measure between two sequences. A commonly used notion of similarity is the number of matches between k -mers ( k -length subsequences) in the two sequences. Extending this definition, by considering two k -mers to match if their distance is at most m , yields better classification performance. This, however, makes the problem computationally much more complex. Known algorithms to compute this similarity have computational complexity that render them applicable only for small values of k and m . In this work, we develop novel techniques to efficiently and accurately estimate the pairwise similarity score, which enables us to use much larger values of k and m , and get higher predictive accuracy. This opens up a broad avenue of applying this classification approach to audio, images, and text sequences. Our algorithm achieves excellent approximation performance with theoretical guarantees. In the process we solve an open combinatorial problem, which was posed as a major hindrance to the scalability of existing solutions. We give analytical bounds on quality and runtime of our algorithm and report its empirical performance on real world biological and music sequences datasets
- Circuit design completion using graph neural networks
Neural Computing and Applications (2023)
- Sequential Graph Neural Networks for Source Code Vulnerability Identification
ArXiv (2023)
- Learning-Based Heuristic for Combinatorial Optimization of the Minimum Dominating Set Problem using Graph Convolutional Networks
ArXiv (2023)
- NeuroGraph: Benchmarks for Graph Machine Learning in Brain Connectomics
ArXiv (2023)
- On augmenting topological graph representations for attributed graphs
Appl. Soft Comput. (2023)
- Resilient distributed vector consensus using centerpoint
Automatica (2022)
- Resilient Multi-agent Reinforcement Learning Using Medoid and Soft-medoid Based Aggregation
2022 IEEE International Conference on Assured Autonomy (ICAA) (2022)
- Data driven smart policing: A novel road distance-based k-median model for optimal substation placement
Comput. Hum. Behav. (2022)
- What a drag! Streamlining the UAV design process with design grammars and drag surrogates
(2022)
- Speech emotion recognition for the Urdu language
Language Resources and Evaluation (2022)
- Attack-Resilient Multi-Agent Flocking Control Using Graph Neural Networks
2022 30th Mediterranean Conference on Control and Automation (MED) (2022)
- Strong structural controllability of networks: Comparison of bounds using distances and zero forcing
Autom. (2022)
- Leader Selection for Strong Structural Controllability in Networks using Zero Forcing Sets
2022 American Control Conference (ACC) (2022)
- Byzantine Resilient Distributed Learning in Multirobot Systems
IEEE Transactions on Robotics (2022)
- Edge Augmentation With Controllability Constraints in Directed Laplacian Networks
IEEE Control Systems Letters (2021)
- Resilient Distributed Vector Consensus Using Centerpoint (cid:63)
(2021)
- DGSD: Distributed graph representation via graph statistical properties
Future Gener. Comput. Syst. (2021)
- Seymour's Second Neighborhood Conjecture for 6-antitransitive digraphs
Discret. Appl. Math. (2021)
- NetKI: A kirchhoff index based statistical graph embedding in nearly linear time
Neurocomputing (2021)
- Optimal school site selection in Urban areas using deep neural networks
Journal of Ambient Intelligence and Humanized Computing (2021)
- Computing Graph Descriptors on Edge Streams
ACM Transactions on Knowledge Discovery from Data (2021)
- Leveraging Deep Learning and SNA approaches for Smart City Policing in the Developing World
Int. J. Inf. Manag. (2021)
- SEMOUR: A Scripted Emotional Speech Repository for Urdu
Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems (2021)
- Optimal school site selection in Urban areas using deep neural networks
Journal of Ambient Intelligence and Humanized Computing (2021)
- Tweet Coupling: a social media methodology for clustering scientific publications
Scientometrics (2020)
- Interpretable multi-scale graph descriptors via structural compression
Inf. Sci. (2020)
- Resilient Distributed Diffusion for Multi-Robot Systems Using Centerpoint
Robotics: Science and Systems XVI (2020)
- Graph-Theoretic Approach for Increasing Participation in Networks With Assorted Resources
IEEE Transactions on Network Science and Engineering (2020)
- Improving Network Robustness through Edge Augmentation While Preserving Strong Structural Controllability
2020 American Control Conference (ACC) (2020)
- A Simpler NP-Hardness Proof for Familial Graph Compression
ArXiv (2020)
- Resilient Vector Consensus in Multi-Agent Networks Using Centerpoints
2020 American Control Conference (ACC) (2020)
- Interplay Between Resilience and Accuracy in Resilient Vector Consensus in Multi-Agent Networks
2020 59th IEEE Conference on Decision and Control (CDC) (2020)
- Resilient multi-robot target pursuit
Proceedings of the 7th Symposium on Hot Topics in the Science of Security (2020)
- Strong Structural Controllability of Diffusively Coupled Networks: Comparison of Bounds Based on Distances and Zero Forcing
2020 59th IEEE Conference on Decision and Control (CDC) (2020)
- Resilient Distributed Vector Consensus Using Centerpoints
(2020)
- Estimating Descriptors for Large Graphs
Advances in Knowledge Discovery and Data Mining (2020)
- Tradeoff Between Controllability and Robustness in Diffusively Coupled Networks
IEEE Transactions on Control of Network Systems (2020)
- Tweet Coupling: a social media methodology for clustering scientific publications
Scientometrics (2020)
- Computation of the Distance-Based Bound on Strong Structural Controllability in Networks
IEEE Transactions on Automatic Control (2019)
- Combinatorial Trace Method for Network Immunization
Inf. Sci. (2019)
- Structural Robustness to Noise in Consensus Networks: Impact of Average Degrees and Average Distances
2019 IEEE 58th Conference on Decision and Control (CDC) (2019)
- On the Trade-off Between Controllability and Robustness in Networks of Diffusively Coupled Agents
2019 American Control Conference (ACC) (2019)
- Influential tweeters in relation to highly cited articles in altmetric big data
Scientometrics (2019)
- Influential tweeters in relation to highly cited articles in altmetric big data
Scientometrics (2019)
- On the Computation of the Distance-based Lower Bound on Strong Structural Controllability in Networks
2019 IEEE 58th Conference on Decision and Control (CDC) (2019)
- Structural Robustness to Noise in Consensus Networks: Impact of Degrees and Distances, Fundamental Limits, and Extremal Graphs
IEEE Transactions on Automatic Control (2019)
- Affine-Invariant Outlier Detection and Data Visualization
None (2017)
- Deep Stylometry and Lexical & Syntactic Features Based Author Attribution on PLoS Digital Repository
None (2017)
- Scalable Approximation Algorithm for Network Immunization
None (2017)
- Spectral Methods for Immunization of Large Networks
ArXiv (2017)
- k-Centerpoints Conjectures for Pointsets in ℝd
Int. J. Comput. Geom. Appl. (2015)
- Network Decontamination with a Single Agent
Graphs and Combinatorics (2015)
- SOME RESULTS IN COMPUTATIONAL AND COMBINATORIAL GEOMETRY
(2014)
- Network Decontamination with a Single Agent
Graphs and Combinatorics (2013)
- Ray-Shooting Depth in R 2 - Algorithms and Applications
(2011)
- Ray-Shooting Depth: Computing Statistical Data Depth of Point Sets in the Plane
None (2011)
- Acceleration of Smith-Waterman using Recursive Variable Expansion
2008 11th EUROMICRO Conference on Digital System Design Architectures, Methods and Tools (2008)
- Acceleration of Biological Sequence Alignment using Recursive Variable Expansion
(2007)
- Efficient Approximation Algorithms for String Kernel Based Sequence Classification
(2017)
Projects
Vitæ
Full Resume in PDF.
-
NeurIPS 2023Area Chair
-
CVPR 2023Area Chair
-
Information Technology University 2022Assocaite Professor - secured Tenure
-
Google Research Scholar Award 2021Economics From Afar
-
Information Technology University 2014 - nowAssistant Professor
Intelligent Machines Lab -
University of Florida 2007-2014PhD. student
CISE: Department of Computer and Information Science and Engineering
Fulbright Scholarship -
Fulbright Scholar 2007-2014PhD. student
-
LUMS 2003 - 2006M.Sc. Student
Department of Computer Sicence
Dean’s Honor List -
Punjab University 2000 - 2002M.Sc. Student
Punjab University College of Information Technology
Gold Medalist
Merit Scholarship -
Punjab University 1999 - 2000P.G.D Student
Department of Comptuer Sicence
First Position in Examination -
Forman Christian College 1997 - 1999F.Sc. Student
Punjab University